不可压N-S方程求解

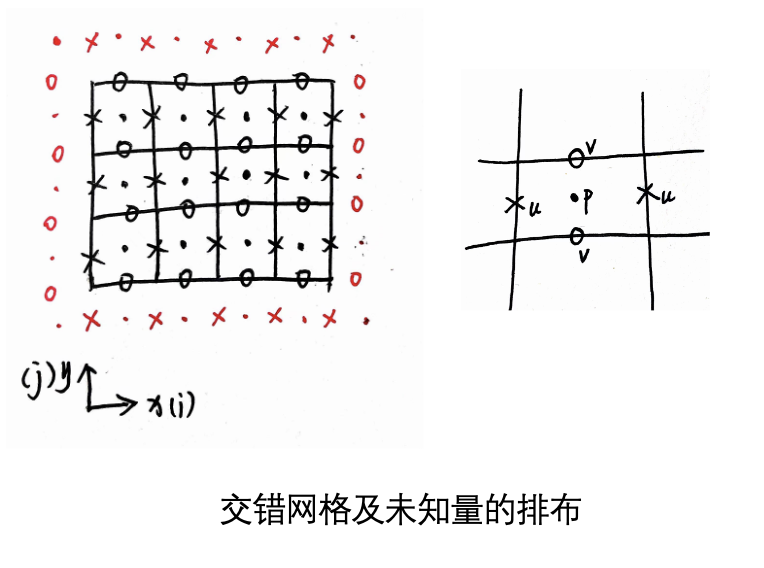
如图所示，总共有$N_x\times N_y$个单元格，压强的未知量个数为$(N_x+2)\times (N_y+2)$，速度分量$u$的未知量个数为$(N_x+1)\times (N_y+2)$，速度分量$v$的未知量个数为$(N_x+2)\times (N_y+1)$。单元格(i,j)的中心的未知量为$p_{i-\frac{1}{2},j-\frac{1}{2}}$，对应数组成员为p[i+1,j+1]，下边界中点为$v_{i-\frac{1}{2},j-1}$v[i+1,j]，上边界中点为$v_{i-\frac{1}{2},j}$v[i+1,j+1]，左边界中点为$v_{i-1,j-\frac{1}{2}}$u[i,j+1]，右边界中点为$v_{i,j-\frac{1}{2}}$u[i+1,j+1]。

边界上的数据存储在一个数组中，那么它们一定是按照[下, 上, 左, 右]的顺序存储的。

投影方法

求解压强

空间离散

$$\Delta p^{n+1}=\rho \left(\frac{\nabla \cdot {\mathbf{u}}^{\ast }-s^{n+1}}{\Delta t}\right)\text{\hspace{1em}(8)}$$ $$(p_b{)}_{i-\frac{1}{2},j-\frac{1}{2}}=\frac{\rho }{\Delta t}\left(\frac{u_{i,j-\frac{1}{2}}-u_{i-1,j-\frac{1}{2}}}{\Delta x}+\frac{v_{i-\frac{1}{2},j}-v_{i-\frac{1}{2},j-1}}{\Delta y}-s_{i-\frac{1}{2},j-\frac{1}{2}}\right)\text{\hspace{1em}(9)}$$ $$\frac{p_{i-\frac{3}{2},j-\frac{1}{2}}-2p_{i-\frac{1}{2},j-\frac{1}{2}}+p_{i+\frac{1}{2},j-\frac{1}{2}}}{h_x^2}+\frac{p_{i-\frac{1}{2},j-\frac{3}{2}}-2p_{i-\frac{1}{2},j-\frac{1}{2}}+p_{i-\frac{1}{2},j+\frac{1}{2}}}{h_y^2}=(b_p{)}_{i-\frac{1}{2},j-\frac{1}{2}}\text{\hspace{1em}(10)}$$

Gauss-Seidel迭代

$$a=\frac{2}{h_x^2}+\frac{2}{h_y^2}$$ $$b=\frac{p_{i-\frac{3}{2},j-\frac{1}{2}}+p_{i+\frac{1}{2},j-\frac{1}{2}}}{h_x^2}+\frac{p_{i-\frac{1}{2},j-\frac{3}{2}}+p_{i-\frac{1}{2},j+\frac{1}{2}}}{h_y^2}-(b_p{)}_{i-\frac{1}{2},j-\frac{1}{2}}$$ $$p_{i-\frac{1}{2},j-\frac{1}{2}}=\frac{b}{a}$$

边界条件

边界索引

四条边界分别为

• 下 $p_{i-\frac{1}{2},-\frac{1}{2}},i\in [1,N_x]$，
• 上 $p_{i-\frac{1}{2},N_y-\frac{1}{2}},i\in [1,N_x]$，
• 左 $p_{-\frac{1}{2},j-\frac{1}{2}},j\in [1,N_y]$，
• 右 $p_{N_x-\frac{1}{2},j-\frac{1}{2}},j\in [1,N_y]$， 其中，四个角点不包含在内。分别对四条边界进行处理：

Dirichlet 类型

• 下 $p_{i-\frac{1}{2},\frac{1}{2}}+p_{i-\frac{1}{2},-\frac{1}{2}}=2g_{i,0}$ , $p_{i-\frac{1}{2},-\frac{1}{2}}=2g_{i-\frac{1}{2},0}-p_{i-\frac{1}{2},\frac{1}{2}}$
• 上 $p_{i-\frac{1}{2},N_y+\frac{1}{2}}+p_{i-\frac{1}{2},N_y-\frac{1}{2}}=2g_{i-\frac{1}{2},N_y}$, $p_{i-\frac{1}{2},N_y+\frac{1}{2}}=2g_{i-\frac{1}{2},N_y}-p_{i-\frac{1}{2},N_y-\frac{1}{2}}$
• 左$p_{\frac{1}{2},j-\frac{1}{2}}+p_{-\frac{1}{2},j-\frac{1}{2}}=2g_{0,j-\frac{1}{2}}$, $p_{-\frac{1}{2},j-\frac{1}{2}}=2g_{0,j-\frac{1}{2}}-p_{\frac{1}{2},j-\frac{1}{2}}$
• 右$p_{N_x+\frac{1}{2},j-\frac{1}{2}}+p_{N_x-\frac{1}{2},j-\frac{1}{2}}=g_{N_x,j}$, $p_{N_x+\frac{1}{2},j-\frac{1}{2}}=g_{0,j-\frac{1}{2}}-p_{N_x-\frac{1}{2},j-\frac{1}{2}}$

Neumann 类型(暂无)

求解速度分量$u$

速度方程为

$$\begin{gathered} \rho \left(\frac{{\mathbf{u}}^{\ast }-{\mathbf{u}}^n}{\Delta t}+{\mathbf{u}}^n\cdot \nabla {\mathbf{u}}^n\right)=\mu \Delta {\mathbf{u}}^{\ast }+{\mathbf{f}}^{n+1} \\ \text{\hspace{1em}(3)} \end{gathered}$$ $$\frac{1}{\Delta t}{\mathbf{u}}^{\ast }-\frac{\mu }{\rho }\Delta {\mathbf{u}}^{\ast }=\frac{1}{\Delta t}{\mathbf{u}}^n+\frac{1}{\rho }{\mathbf{f}}^{n+1}-{\mathbf{u}}^n\cdot \nabla {\mathbf{u}}^n\text{\hspace{1em}(7)}$$

先去掉对流项

$$\frac{1}{\Delta t}{\mathbf{u}}^{\ast }-\frac{\mu }{\rho }\Delta {\mathbf{u}}^{\ast }=\frac{1}{\Delta t}{\mathbf{u}}^n+\frac{1}{\rho }{\mathbf{f}}^{n+1}\text{\hspace{1em}(7)}$$

空间离散

$$\frac{1}{\Delta t}{u}_{i,j-\frac{1}{2}}^{\ast }-\frac{\mu }{\rho }\left(\frac{u_{i-1,j-\frac{1}{2}}^{\ast }-2u_{i,j-\frac{1}{2}}^{\ast }+u{\ast }_{i+1,j-\frac{1}{2}}^{\ast }}{h_x^2}+\frac{u_{i,j-\frac{3}{2}}{-2u_{i,j-\frac{1}{2}}^{\ast }}^{\ast }+u_{i,j+\frac{1}{2}}^{\ast }}{h_y^2}\right)=(b_1{)}_{i,j-\frac{1}{2}}\text{\hspace{1em}(3.1)}$$

Gauss-Seidel迭代

$$\left[\frac{1}{\Delta t}+\frac{2\mu }{\rho }\left(\frac{1}{h_x^2}+\frac{1}{h_y^2}\right)\right]u_{i,j-\frac{1}{2}}^{\ast }={\left(b_1\right)}_{i,j-\frac{1}{2}}+\frac{\mu }{\rho }\left(\frac{u_{i-1,j-\frac{1}{2}}^{\ast }+u_{i+1,j-\frac{1}{2}}^{\ast }}{h_x^2}+\frac{u_{i,j-\frac{3}{2}}^{\ast }+u_{i,j+\frac{1}{2}}^{\ast }}{h_y^2}\right)\text{\hspace{1em}(3.2)}$$

其中

$$(b_1{)}_{i,j-\frac{1}{2}}=\frac{1}{\Delta t}{u}_{i,j-\frac{1}{2}}^n+\frac{1}{\rho }(f_1{)}_{i,j-\frac{1}{2}}^{n+1}$$

边界索引

方程(3.1)中，$u_h$的个数为$N_x+1\times N_y+2$，四条边界分别为

• 下 $u_{i,-\frac{1}{2}},i\in [0,N_x]$
• 上 $u_{i,N_y+\frac{1}{2}},i\in [0,N_x]$
• 左 $u_{0,j-\frac{1}{2}},j\in [0,N_y+1]$
• 右 $u_{N_x,j-\frac{1}{2}},j\in [0,N_y+1]$ 其中，四个角点分别包含在左右两条边界中。

Dirichlet类型

• 下 $u_{i,\frac{1}{2}}+u_{i,-\frac{1}{2}}=2g_{i,0}$ , $u_{i,-\frac{1}{2}}=2g_{i,0}-u_{i,\frac{1}{2}}$
• 上 $u_{i,N_y+\frac{1}{2}}+u_{i,N_y-\frac{1}{2}}=2g_{i,N_y}$, $u_{i,N_y+\frac{1}{2}}=2g_{i,N_y}-u_{i,N_y-\frac{1}{2}}$
• 左 $u_{0,j-\frac{1}{2}}=g_{0,j-\frac{1}{2}}$
• 右 $u_{N_x,j-\frac{1}{2}}=g_{N_x,j-\frac{1}{2}}$

Neumann类型

• 下 $\frac{u_{i,\frac{1}{2}}-u_{i,-\frac{1}{2}}}{h_y}=g_{i,0}$, $u_{i,-\frac{1}{2}}=u_{i,\frac{1}{2}}-h_y{g}_{i,0}$
• 上$\frac{u_{i,N_y+\frac{1}{2}}-u_{i,N_y-\frac{1}{2}}}{h_y}=g_{i,N_y}$, $u_{i,N_y+\frac{1}{2}}=u_{i,N_y-\frac{1}{2}}+h_y{g}_{i,N_y}$
• 左 $\frac{u_{1,j-\frac{1}{2}}-u_{-1,j-\frac{1}{2}}}{2h_x}=g_{0,j-\frac{1}{2}}$, $u_{\text{ghost}}=u_{-1,j-\frac{1}{2}}=u_{1,j-\frac{1}{2}}-2h_x{g}_{0,j}$

$$u_{0,j-\frac{1}{2}}=\frac{(u_{\text{ghost}}+u_{1,j-\frac{1}{2}})h_y^2+(u_{0,j-\frac{3}{2}}+u_{0,j-\frac{1}{2}})h_x^2-h_x^2{h}_y^2{f}_{0,j-\frac{1}{2}}}{2h_y^2+2h_x^2},$$

• 右 $\frac{u_{N_x+1,j-\frac{1}{2}}-u_{N_x-1,j-\frac{1}{2}}}{2h_x}=g_{N_x,j-\frac{1}{2}}$, $u_{\text{ghost}}=u_{N_x+1,j-\frac{1}{2}}=u_{N_x-1,j-\frac{1}{2}}+2h_x{g}_{N_x,j}$

$$u_{N_x,j-\frac{1}{2}}=\frac{(u_{N_x+1,j-\frac{1}{2}}+u_{\text{ghost}})h_y^2+(u_{N_x,j-\frac{3}{2}}+u_{N_x,j-\frac{1}{2}})h_x^2-h_x^2{h}_y^2{f}_{N_x,j-\frac{1}{2}}}{2h_y^2+2h_x^2},$$