投影方法

不可压流体可用splitting step method)求解，文献中也常称之为投影方法(projection method)。投影方法可以分为三类：

• pressure correction method
• velocity correction method
• consistent splitting method

不可压流体的速度和压强通过不可压约束耦合在一起，在数值模拟中这是一个难点。投影方法可以将原问题解偶成一系列椭圆问题，进而高效求解。

在讨论分投影方法前，我们要知道N-S方程的非线性项不会影响分裂误差的收敛率，如果解是正则的，那么关于Stokes方程的结论对N-S方程也是适用的。Stokes方程比N-S方程少一项对流项。

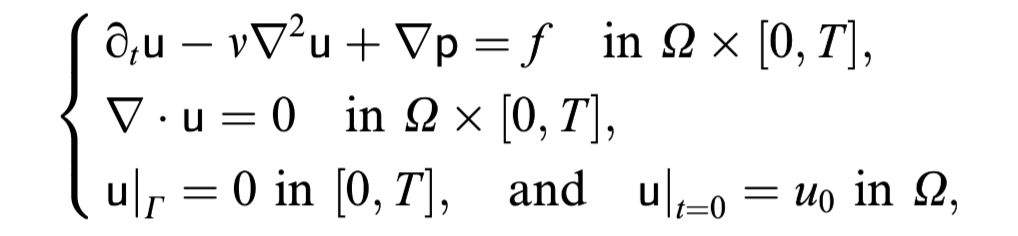
1. pressure correction method

• 向后欧拉方法 分两步进行，第一步先通过忽略压强或显式处理压强算出一个临时速度，第二步通过投影方法修正速度和压强。

1.1 non-incremental pressure-correction scheme

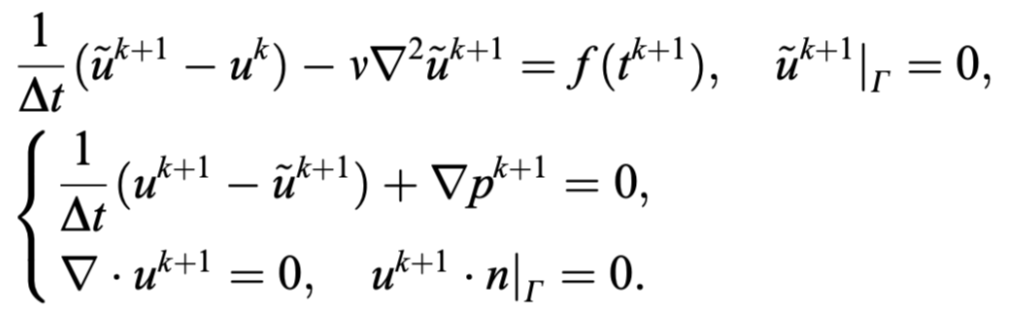假设解$(\mathbf{u},p)$足够光滑，有如下误差估计

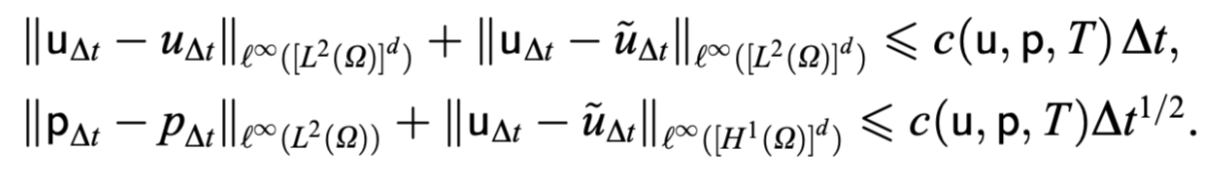
注意点：

• 强制施加边界条件$\nabla p\cdot \mathbf{n}{|}_{\partial \Omega }=0$，这是人工Neumann边界条件(artificial Neumann boundary condition)，它导致解存在数值边界层(numerical boundary layer)，使速度无法依$H^1$范数一阶收敛，压强无法依$L^2$范数一阶收敛。
• 分裂误差为$O(\Delta t)$，${\partial }_t-\nu {\nabla }^2$即使使用更高阶的逼近也不能提高整体精度。

1.2 The standard incremental pressure-correction schemes

incremental pressure-correction scheme in standard form IPCS 通过之前时刻的压强修正当前时刻的压强，以此来获得更高精度的压强。

• BDF2(Backward Difference Formula of second-order)方法

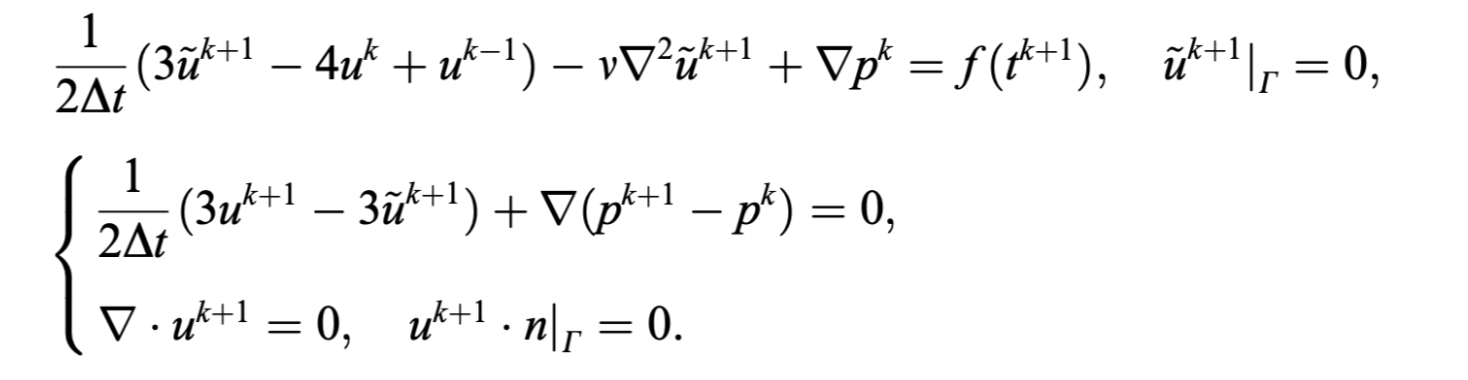
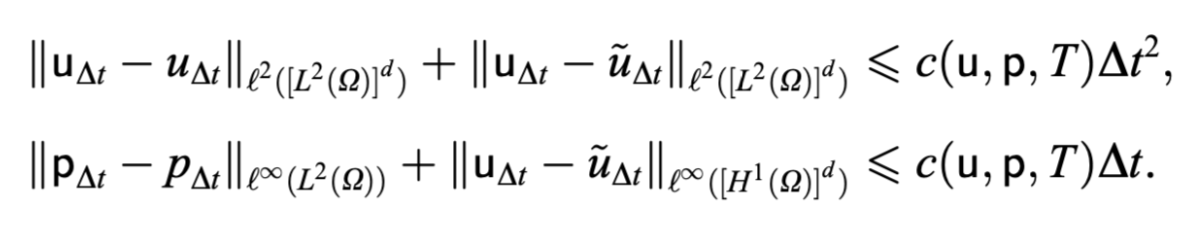
注意：

• 速度依$L^2$范数二阶收敛
• 人工边界条件$\nabla (p^{k+1}-p^k)\cdot \mathbf{n}{|}_{\partial \Omega }=0$使速度无法依$H^1$二阶收敛，压强无法依$L^2$二阶收敛。
• 由于分裂误差的存在，使用高于二阶的时间离散格式无法提高精度。

1.3 rotational incremental pressure-correction schemes

• 克服了人工Neumann边界条件，压力精度提高了半阶